In Chapter 7 Wild and Seber call these ``two standard error intervals,'' but in Chapter 8 we find out they are really called confidence intervals.
The thingies discussed in this section are called interval estimates.
For contrast, the estimates previously discussed, like ![]() and
and ![]() are called point estimates.
are called point estimates.
For any point estimate having an approximately normal sampling distribution
Generically,
And
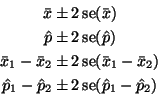
Plugging in the formulas for the standard errors,
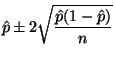
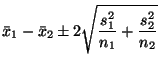
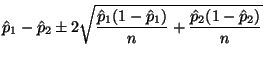
For confidence levels other than 95% see Section 1.4.4 below.
Nothing in the preceeding section is useful for small samples. For proportions there is no small sample theory. But for means there is. In Chapter 7 we only do the one-sample case (the two-sample case will come later).
The confidence interval for ![]() in the preceeding section, was derived
from the fact that
in the preceeding section, was derived
from the fact that
The difference between the two theories is that
The relation between (1) and the confidence interval is that the two equations
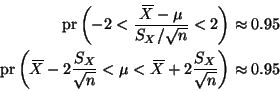
Hence in order to get exact (not approximate) confidence intervals
assuming a normal population distribution we only need to substitute
for 2 the ![]() such that
such that
The ![]() critical values for 95% confidence are given in the column
headed 0.025 of Appendix 6 in Wild and Seber or by either of
the R commands
critical values for 95% confidence are given in the column
headed 0.025 of Appendix 6 in Wild and Seber or by either of
the R commands
qnorm(0.975, n - 1) - qnorm(0.025, n - 1)where n is the sample size (so n - 1 is the degrees of freedom).
For example, if ![]() , then
, then
For confidence levels other than 95% see Section 1.4.4 below.
For confidence levels other than 95%, just change the 0.95 in (3) to some other number.
To get
theconfidence
theorquantile of the Student
distribution
minus theThusquantile of the Student
distribution.
| confidence level | column of Appendix 6 headed |
| 90% | 0.05 |
| 95% | 0.025 |
| 99% | 0.005 |
The same trick works for large-sample intervals based on the approximate
normality of the sampling distribution of a point estimate. Just use
the
Normal![]() distribution instead of the
Student
distribution instead of the
Student![]() distribution. This the Student's
distribution. This the Student's ![]() -distribution with
``infinity degrees of freedom'' in the bottom row of Appendix 6 in Wild and
Seber. Hence
-distribution with
``infinity degrees of freedom'' in the bottom row of Appendix 6 in Wild and
Seber. Hence
| confidence level | |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
Note also that a finicky person also uses 1.96 s. e. intervals rather than 2 s. e. intervals for 95% confidence (not that it really matters, it's only approximate anyway).