Homework Solutions #12
If X is symmetric about m, then m is the median. If l and uare the lower and upper quartiles, then
u - m = m - l, again by symmetry.
Define s = u - m. Then
The standard normal distribution is symmetric about zero, hence the median is m = 0. Hence the MAD is half the interquartile range by part (a). The upper quartile is u = 0.6745 by linear interpolation in Table I in the Appendix of Lindgren. Hence that's the MAD ( s = u - m = u, since m = 0).
The median is 80 [answer to 7-4(c)]. The sorted absolute deviations from
the median are
The density of X is
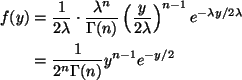
The median is ![]() by symmetry, and
by symmetry, and
![]() .
Hence the asymptotic variance given by Corollary 7.28 in the notes is
.
Hence the asymptotic variance given by Corollary 7.28 in the notes is
![]()
Again the median is ![]() by symmetry, but now
by symmetry, but now
![]() .
Hence the asymptotic variance is
.
Hence the asymptotic variance is
![]()
To apply the hint for part (a), we need to find the distribution of X(n),
which is the case k = n of formula (7.35) in the notes
The hint says we should show that (1) converges to the c. d. f. of
the distribution concentrated at ![]() .
What is that? The probability
at
.
What is that? The probability
at ![]() is the size of the jump of the c. d. f. at
is the size of the jump of the c. d. f. at ![]() .
A constant
random variable is concentrated at one point, hence puts probability one
at that point. Thus the c. d. f. must jump from zero to one at that point
.
A constant
random variable is concentrated at one point, hence puts probability one
at that point. Thus the c. d. f. must jump from zero to one at that point
It is easily checked that indeed (1) converges to (2),
that
To apply the hint for part (a), we need to find the c. d. f. of Yn
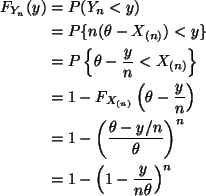
Or, being more precise, using the fact that Yn ranges from zero when
![]() to
to ![]() when
X(n) = 0,
when
X(n) = 0,
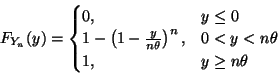
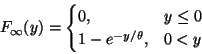
Not all asymptotic distributions are normal. Not all asymptotics go at
``rate'' ![]() .
Here we have
.
Here we have
This is not the only example of ``nonstandard'' asymptotics. In fact,
extreme values always have nonstandard asymptotics. The only reason for
doing the
![]() case here is because the calculations
are easiest for it.
case here is because the calculations
are easiest for it.
By Theorem 7.24 in the notes or Theorem 11 in Chapter 7 in Lindgren
R gives the more precise answer
> 1 - pchisq(18, 9) [1] 0.03517354
Use Theorem 7 of Chapter 3 in Lindgren (the change-of-variable theorem
in the special case of a linear transformation). This gives in the
case
![]()
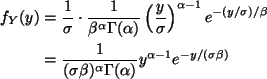
One could argue as in part (a), but an even simpler way to do the
problem is just to make the substitution
![]() in all the formulas of the problem. This obviously gives the desired
result. You don't even have to write it out to see it.
in all the formulas of the problem. This obviously gives the desired
result. You don't even have to write it out to see it.
We are to calculate
![]() .
Before we do that
we need
.
Before we do that
we need
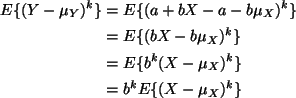
We need to calculate
![]() and
and ![]() for the
for the
![]() distribution. We know that
distribution. We know that
![]() .
The fourth central
moment is fairly obnoxious if done by hand
.
The fourth central
moment is fairly obnoxious if done by hand
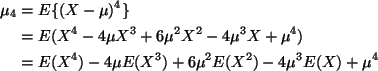
by linearity of expectation. Now we can use the gamma integral
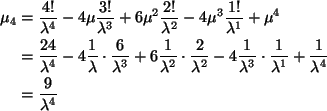
In[1]:= f[x_] = lambda Exp[- lambda x]
lambda
Out[1]= ---------
lambda x
E
In[2]:= mu = Integrate[ x f[x], {x, 0, Infinity},
Assumptions -> {Re[lambda] > 0} ]
1
Out[2]= ------
lambda
In[4]:= mu4 = Integrate[ (x - mu)^4 f[x], {x, 0, Infinity},
Assumptions -> {Re[lambda] > 0} ]
9
Out[4]= -------
4
lambda
Either way we get