Homework Solutions #10
Let
Yi = Xik, then Y1, Y2, ![]() is a sequence of independent
identically distributed random variables (functions of independent random
variables are independent by Theorem 13 of Chapter 3 in Lindgren) with
expectation
is a sequence of independent
identically distributed random variables (functions of independent random
variables are independent by Theorem 13 of Chapter 3 in Lindgren) with
expectation
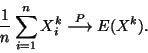
Write Y for the weight of the 100 booklets. Then
Let
![]() be one error, then from the appendix
on brand name distributions
be one error, then from the appendix
on brand name distributions
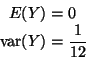
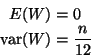
Thus
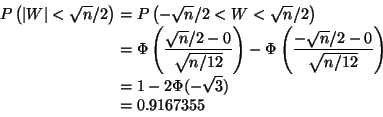
By direct count, the probability of a sum of 5 or less
rolling a pair of dice is 5/18. Thus, if Y is the number of such rolls
in 72 tries,
![]() ,
and
,
and
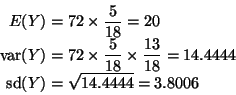
So, using a continuity correction,
From a picture of the triangular density, the two inside intervals have
three times the probability of the outside intervals. Thus the probabilities
of the intervals are
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
.
Let X1, X2, X3, and X4 be the counts in the cells (1, 2, 2, 1),
then this is a multinomial random vector and the probability of these counts
is
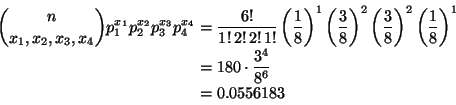
Since it is a linear transformation of a multivariate normal random vector,
(X, Y) is also multivariate normal with mean vector zero because
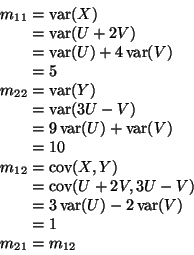
From the variance formula for the multinomial in the appendix on brand name
distributions
![\begin{displaymath}\begin{split}
\mathop{\rm var}\nolimits(X_i - X_j)
& =
\ma...
... p_i p_j
\\
& =
n [ p_i + p_j - (p_i - p_j)^2 ]
\end{split}\end{displaymath}](img19.gif)
The problem is to specialize the formula
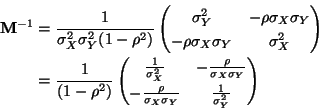
The constant part of the density is now done
In general a quadratic form is written out explicitly in terms of components as
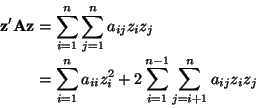
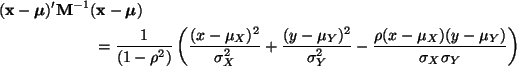
In this case the elements of the partitioned variance matrix are all scalars
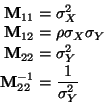
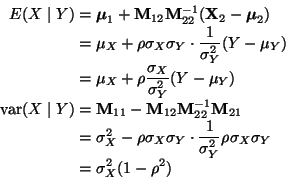
We are to calculate
![]() for given d,
where
for given d,
where
Write
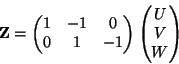
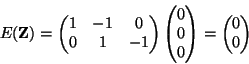
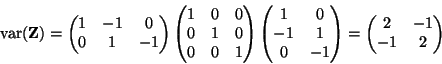
From the formula for the variance,
![\begin{displaymath}\mathop{\rm var}\nolimits(Z_1 \mid Z_2)
=
2 \left[1 - \left(- \frac{1}{2}\right)^2 \right]
=
\frac{3}{2}
\end{displaymath}](img47.gif)