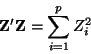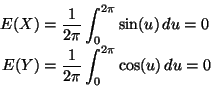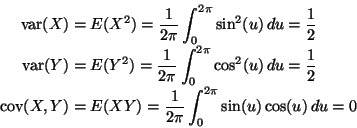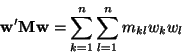Up: Stat 5101 Homework Solutions
Statistics 5101, Fall 2000, Geyer
Homework Solutions #9
A general normal random variable
X has the
form
X= a+ BZ,
where
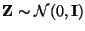 .
In order for
X to have
mean zero, we need
a= 0. Thus
X= BZ,
and in order for
X to be nondegenerate,
B must be invertible,
in which case
.
In order for
X to have
mean zero, we need
a= 0. Thus
X= BZ,
and in order for
X to be nondegenerate,
B must be invertible,
in which case
and
M-1 = (B')-1 B-1
and
Q
=
X' M-1 X
=
X' (B')-1 B-1 X
=
Z' Z
because
Z= B-1 X.
Now
is the sum of squares of p independent standard normal random variables,
hence
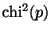 distributed.
Using R for the computer work
distributed.
Using R for the computer work
> M <- matrix(c(3, 2, -1, 2, 3, 2, -1, 2, 3), nrow=3)
> M
[,1] [,2] [,3]
[1,] 3 2 -1
[2,] 2 3 2
[3,] -1 2 3
> eigen(M)
$values
[1] 5.3722813 4.0000000 -0.3722813
$vectors
[,1] [,2] [,3]
[1,] 0.4544013 -7.071068e-01 -0.5417743
[2,] 0.7661846 -1.155753e-16 0.6426206
[3,] 0.4544013 7.071068e-01 -0.5417743
The negative eigenvalue
-0.3722813 means this is not a positive
semi-definite matrix, hence not a variance matrix.
Using R for the computer work
> M <- matrix(c(3, 2, -1/3, 2, 3, 2, -1/3, 2, 3), nrow=3)
> M
[,1] [,2] [,3]
[1,] 3.0000000 2 -0.3333333
[2,] 2.0000000 3 2.0000000
[3,] -0.3333333 2 3.0000000
> eigen(M)
$values
[1] 5.666667 3.333333 0.000000
$vectors
[,1] [,2] [,3]
[1,] 0.4850713 -7.071068e-01 -0.5144958
[2,] 0.7276069 -2.473336e-19 0.6859943
[3,] 0.4850713 7.071068e-01 -0.5144958
Since all three eigenvalues are nonnegative, this is a possible covariance
matrix, but since one of the eigenvalues is zero,
M is not positive
definite and the random variable is degenerate.
The only hard thing about this problem is realizing it is simple
(and perhaps looking up how to integrate trig functions).
Hence the mean vector is zero. Then
So
Not part of the problem, but we have here another example that uncorrelated
does not imply independent.
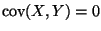 ,
but having a degenerate
joint distribution, X and Y are highly dependent. Indeed, since
the vector (X, Y) is concentrated on the unit circle,
X2 + Y2 = 1
with probability one (essentially because of the trig identity
,
but having a degenerate
joint distribution, X and Y are highly dependent. Indeed, since
the vector (X, Y) is concentrated on the unit circle,
X2 + Y2 = 1
with probability one (essentially because of the trig identity
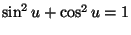 for
all u). Thus the conditional distribution of Y given X is concentrated
at the two points
for
all u). Thus the conditional distribution of Y given X is concentrated
at the two points
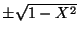 .
So X almost determines Y
(it determines the absolute value, only the sign is still random).
In general
.
So X almost determines Y
(it determines the absolute value, only the sign is still random).
In general
If we choose
w so that only wi and wj are nonzero, this becomes
mi i wi2 + 2 mi j wi wj + mj j wj2
and this must be nonnegative for any choice of wi and wj
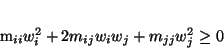 |
(1) |
Try
Then (1) becomes
which implies one of the inequalities to be proved. If instead make
wj negative, we get the same thing with a minus sign on the middle
term, and that proves the other inequality.
If the dimension is n = 1, then the variance matrix is just a scalar
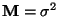 and
and
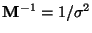 and
and
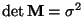 .
Making all these changes turns
(5.24) on p. 144 of the notes into (9) on p. 180 in Lindgren.
A vector
X concentrated at the point
a has
.
Making all these changes turns
(5.24) on p. 144 of the notes into (9) on p. 180 in Lindgren.
A vector
X concentrated at the point
a has
(the variance matrix being the zero matrix). Our definition of multivariate
normal says there is a multivariate normal random vector with this mean and
variance, namely the vector
Y= a+ BZ,
where
Z is a standard multivariate normal random vector and we choose
B to also be the zero matrix. Clearly
Y is also concentrated
at
a and thus is equal to
X with probability one.
Any linear transformation of multivariate normal is again multivariate normal
(Theorem 12 of Chapter 12 in Lindgren, inexplicably omitted from the notes).
Thus
Y is multivariate normal. Hence to figure out which normal, we
only need to find its parameters (mean vector and variance matrix).
Thus
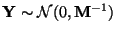 .
.



Up: Stat 5101 Homework Solutions
Charles Geyer
2000-11-14