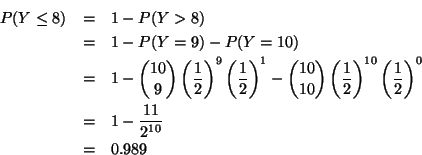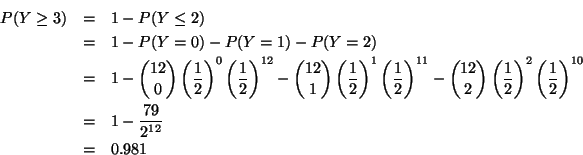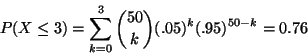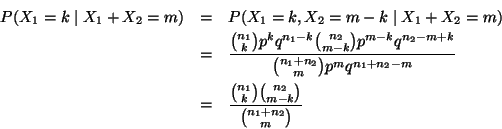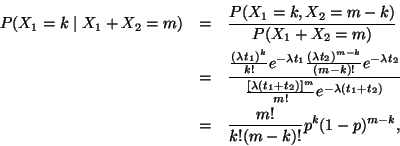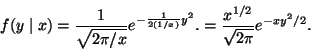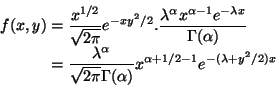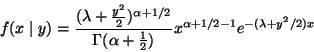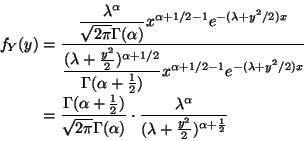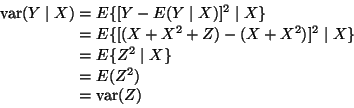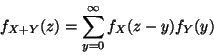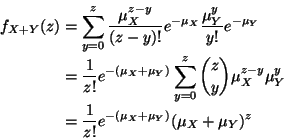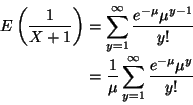Up: Stat 5101 Homework Solutions
Statistics 5101, Fall 2000, Geyer
Homework Solutions #7
Let Y be the r. v. denoting the number of successes in four trials.
Then
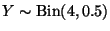 .
.
Since
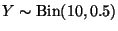 ,
,
Since
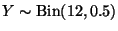 ,
,
Assuming independent trials, the results of the preceding three trials are
irrelevant.
Since
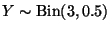 ,
,
Since
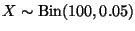 ,
,
and
Since
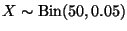 ,
,
That is,
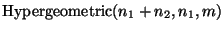 .
Let U denote the number of trials required to obtain the r-th success;
then
.
Let U denote the number of trials required to obtain the r-th success;
then
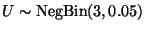 .
Hence
.
Hence
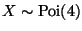 .
So
.
So
The average number in 1/4 min is
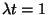 .
Hence
.
Hence
The average number in 1/2 min is
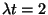 .
Hence
.
Hence
P(X = 0) = e-2 = 0.1353
There are 30 arrivals per hour, or 2.5 per minute, so
X1 and X2 are independent,
so
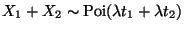 .
Then
.
Then
where
p = t1 / (t1 + t2). Hence the conditional distribution is
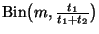 .
The conditional density of Y given X is
.
The conditional density of Y given X is
The marginal density of X is
Thus the joint density is (marginal times conditional)
It is clear from the form that this, considered as a function of x for
fixed y is proportional to a
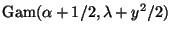 density. Thus that is the conditional distribution.
The conditional density is
density. Thus that is the conditional distribution.
The conditional density is
The marginal is joint over conditional
Just another way of describing part (a). The conditional expectation is
the best prediction.
Just another way of describing part (d). The expected squared prediction
error of the best prediction is
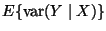 ,
which in this case
is the same as
,
which in this case
is the same as
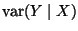 ,
because the conditional variance is not
actually a function of X.
The convolution formula is
,
because the conditional variance is not
actually a function of X.
The convolution formula is
(Theorem 1.7 in the notes with the integral replaced by a sum because Y
is discrete). But the sum actually only goes from 0 to z because x = z - y
must be nonnegative. Thus
which is the
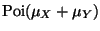 density.
The count has a
density.
The count has a
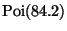 distribution. So is variance is
84.2 and its standard deviation is
distribution. So is variance is
84.2 and its standard deviation is
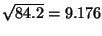 .
.
Do the change of variables y = x + 1. Then
The sum now looks like the sum of a Poisson density equaling one except that
the y = 0 term is missing. Thus the sum is one minus the y = 0 term
and the answer is A times this, since A is a constant.



Up: Stat 5101 Homework Solutions
Charles Geyer
2000-11-14