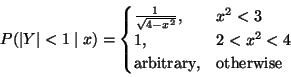Homework Solutions #6
The joint density function of X and Y, is
The marginal density for X is then
One conditional density function is
Since X and Y are independent,
By Theorem 10 (p. 72) in Lindgren and also by the section on
``conditional probability as renormalization'' in the notes,
the conditional distributions of a uniform distribution are uniform.
Hence
![]() ,
and the mean of this distribution is
,
and the mean of this distribution is
![]() .
.
Nothing easy here, have to just do it,
![\begin{displaymath}\begin{split}
E\{(Y - X)^2\}
& =
\int_0^1 \int_0^y (y - x)...
...t[ \frac{y^4}{4} \right]_0^1
\\
& =
\frac{1}{6}
\end{split}\end{displaymath}](img9.gif)
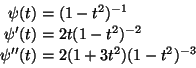
So
If
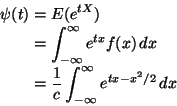
First we ``complete the square'' in the exponent
From (2.61), the marginal density of X is
Now since,
In (2.62) the domains of integration depend on the other variable.
The marginal density of X is
By the definition of independence, equation (2.58) in the notes,
E(X Y) = E(X) E(Y). Hence
E(X) = 0 because X is symmetric about 0, and
E(X Y) = E(X3) = 0. By the symmetry of X and
Theorem 2.10.
Thus
As the hint says, there exists an event A such that
![]() .
If X were independent of itself, then we would have
.
If X were independent of itself, then we would have
First note that
![]() ,
just by definition of these
notations. Then
,
just by definition of these
notations. Then
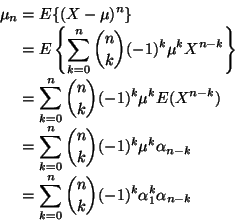
To apply the same trick to
![]() ,
we first need to express
X as a binomial, and, in order to eventually produce
,
we first need to express
X as a binomial, and, in order to eventually produce
![]() terms,
the binomial must involve
terms,
the binomial must involve ![]() ,
thus the obvious expression
,
thus the obvious expression
![\begin{displaymath}\begin{split}
\alpha_n
& =
E\{[(X - \mu) + \mu]^n\}
\\
...
...=
\sum_{k = 0}^n \binom{n}{k} \alpha_1^k \mu_{n-k}
\end{split}\end{displaymath}](img35.gif)
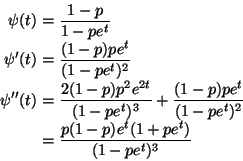
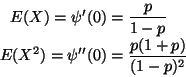
If the integral exists, the function is
Note: The formula for ![]() produces a completely ridiculous
result when
produces a completely ridiculous
result when
![]() ,
saying that the integral of a positive function
is negative. Thus it is important to check whether integrals exist.
The formalism of doing the indefinite integral and plugging in the limits
won't tell when what you are doing is completely wrong!
,
saying that the integral of a positive function
is negative. Thus it is important to check whether integrals exist.
The formalism of doing the indefinite integral and plugging in the limits
won't tell when what you are doing is completely wrong!
The joint density is
By the principle that the conditionals of a uniform are uniform,
this is some one-dimensional uniform distribution. The only issue is
to figure out the ranges. The range of x when y is fixed
consists of the x such that
x2 + y2 < 4, which is
Since
![]() ,
,
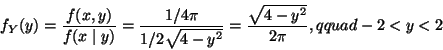
From part(a), the distribution of ![]() is symmetric about zero,
so has mean zero.
is symmetric about zero,
so has mean zero.
This is tricky because it involves case splitting.
For x near ![]() ,
the entire range of the distribution of
,
the entire range of the distribution of ![]() lies between + 1 and - 1.
Hence in this case
lies between + 1 and - 1.
Hence in this case
![]() .
.
For x near 0, the interval (-1, 1) is a proper subinterval of the
range of ![]() ,
and the probability is the area under the density
over this interval, which is just base times height (the area of a rectangle).
Hence in this case
,
and the probability is the area under the density
over this interval, which is just base times height (the area of a rectangle).
Hence in this case