Statistics 5101, Fall 2000, Geyer

Homework Solutions #4

Problem 4-8

(a)

This density is symmetric about 0, which is thus the mean.

(b)

This density is symmetric about 0, which is thus the mean.

(c)

This density is symmetric about 1/2, which is thus the mean.

Problem 4-44

(a)

$$\mathop{\rm var}\nolimits(2X + 3Y - Z) = 2^2 \mathop{\rm va... ...\rm var}\nolimits(Y) + 1^2 \mathop{\rm var}\nolimits(Z) = 14$$

(b)

$$\mathop{\rm cov}\nolimits(X - 2Y, 3X + Y + 2Z) = \mathop{\r... ...hop{\rm var}\nolimits(X) - 2 \mathop{\rm var}\nolimits(Y) = 1$$

The other covariances vanish, because X, Y and Zare independent.

Problem 4-49

$$\begin{align*}\mathop{\rm cov}\nolimits(X+Y, X-Y) & = \mathop{\rm cov}\nolimit... ... & = \mathop{\rm var}\nolimits(X) - \mathop{\rm var}\nolimits(Y) \end{align*}$$
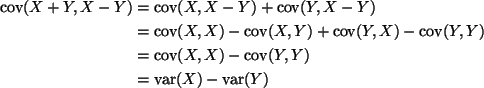
and this equals zero if and only if $\sigma_X = \sigma_Y$.

Problem N2-3

Take a=1 and b = -1 in Theorem 2.1 (linearity of expectation).

Problem N2-5

$$\begin{align*}E(X{\mkern -13.5 mu}\overline{\phantom{\text{X}}}_n) & = E\left(... ...s + E(X_n) \bigr] \\ & = \frac{1}{n} \cdot n \mu \\ & = \mu \end{align*}$$

Problem N2-10

There are two things to be proved. First, since X - a and a - Xare equal in distribution, they have the same moments, in particular,
$$\begin{align*}E(X - a) & = E(a - X) \\ E(X) - a & = a - E(X) \\ 2 E(X) & = 2 a \\ E(X) & = a \end{align*}$$
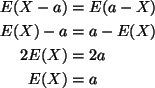
That proves the first part.

The second part starts the same way except with k-th moments for k odd.
$$\begin{align*}E\{(X - a)^3\} & = E\{(a - X)^3\} \\ E\{(X - a)^3\} & = E\{- (X - a)^3\} \\ E\{(X - a)^3\} & = - E\{(X - a)^3\} \end{align*}$$
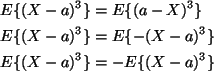
because (- 1)^k = - 1 if k is odd. Since the only number that is its own negative is zero,

$$E\{(X - a)^3\} = 0,$$

and this is what was to be proved because $\mu = a$ by the first part, so this is the k-th central moment.

Problem N2-11

(a)

The inverse transformation X = a + Y has derivative 1, so

f_Y(y) = f_X(a + y)

(b)

The inverse transformation X = a - Z has derivative - 1, so

f_Z(z) = f_X(a - z)

(c)

The two functions defined in parts (a) and (b) are the same if and only if they have the same values for the same argument, say t
$$\begin{align*}f_Y(t) & = f_Z(t) \\ f_X(a + t) & = f_X(a - t) \end{align*}$$
which is what was to be proved.

Problem N2-12

(all parts)

Since these are symmetric distributions, the medians are the same as the means calculated in Problem 4-8.

Problem N2-14

(a)

Since X is either zero or one and 0^k = 0 and 1^k = 1 for all k, it follows that X^k = X for all k, and

$$E(X^k) = E(X) = \mu$$

(b)

Since $0 \le X \le 1$, it follows that

$$0 \le E(X) \le 1$$

by monotonicity of probability (Theorem 2.8 in the notes).

(c)

$$\mathop{\rm var}\nolimits(X) = E(X^2) - E(X)^2 = \mu - \mu^2 = \mu (1 - \mu)$$

Problem N2-16

$$\mathop{\rm var}\nolimits\left(\sum_{i=1}^n a_i X_i\right) = \sum_{i=1}^n a_i^2 \mathop{\rm var}\nolimits(X_i)$$

(the covariance terms are all zero if the variables are uncorrelated).

Problem N2-17

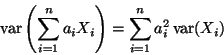
Note: There is no need to do this problem if you do N2-17 first. Both parts are special cases of the general formula derived in N2-17. Conversely, if you do this first, N2-17 can be done easily.

The first part:

$$E(Z) = E\left(\frac{X-\mu}{\sigma}\right) = \frac{\mu-\mu}{\sigma} = 0$$

and

$$\mathop{\rm var}\nolimits(Z) = \mathop{\rm var}\nolimits\le... ...frac{X-\mu}{\sigma}\right) = \frac{\sigma^2}{\sigma^2} = 1$$

The second part:

$$E(X) = E(\mu + \sigma Z) = \mu + \sigma E(Z) = \mu + \sigma \cdot 0 = \mu$$

and

$$\mathop{\rm var}\nolimits(X) = \mathop{\rm var}\nolimits(\m... ...igma^2 \mathop{\rm var}\nolimits(Z) = \sigma^2 \cdot 1 = 1$$

Problem N2-18

We need to solve the equations
$$\begin{align*}\mu_{Y} & = a + b \mu_{X} \\ \sigma_{Y}^{2} & = b^2 \sigma_{X}^2 \end{align*}$$
for a and b. Solve the second and then plug into the first
$$\begin{align*}b & = \frac{\sigma_Y}{\sigma_X} \\ a & = \mu_Y - b \mu_X = \mu_Y - \frac{\sigma_Y}{\sigma_X} \mu_X \end{align*}$$

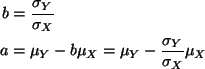
On the other hand, we could have used the solution to N2-17. First standardize, then ``unstandardize''

$$Y = \mu_Y + \sigma_Y Z = \mu_Y + \sigma_Y \frac{X - \mu_X}{\sigma_X} = \mu_Y + \frac{\sigma_Y}{\sigma_X} (X - \mu_X)$$

which is the same solution as obtained by solving simultaneous equations.