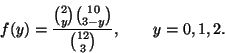Homework Solutions #2
Note: Original done by Laura Pontiggia, Fall 1999. Additions by Yumin Huang, Fall 2000.
Since
![]() ,
and since
,
and since
![]() [using prop. (7)] then
[using prop. (7)] then
![]() .
Using prop. (1):
.
Using prop. (1):
![]() .
.
The inequality on the right (the only one we were asked to do)
![]() follows from
Property (3) and Axiom 1.
follows from
Property (3) and Axiom 1.
By Theorem 2,
![]() .
Since
.
Since
![]() is nonnegative. The inequality
holds for n = 2.
is nonnegative. The inequality
holds for n = 2.
Now, assume the inequality holds when n = k - 1. Let
![]() .
Applying Theorem 2(3) again, it follows
that
.
Applying Theorem 2(3) again, it follows
that
![]() .
Therefore the
inequality holds by mathematical induction.
.
Therefore the
inequality holds by mathematical induction.
Since each characteristic two possible values, the number of outcomes in this experiment is 42=16.
The probability distribution that reflects the proportions 9:3:3:1 is
![]() .
Hence the probability that a plant has yellow peas is given by
.
Hence the probability that a plant has yellow peas is given by
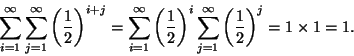
Call the event in question A, so
| Y | 1 | 2 | 3 | 4 | f(x) | |
| X | ||||||
| 1 | 0 |
|
|
|
|
|
| 2 |
|
0 |
|
|
|
|
| 3 |
|
|
0 |
|
|
|
| 4 |
|
|
|
0 |
|
|
| f(y) |
|
|
|
|
1 |
The distribution is uniform (equally likely outcomes) except for the outcomes on the diagonal (with X = Y), which are impossible because of the sampling ``without replacement.''
| X | 1 | 2 | 3 | 4 |
| fX(x) |
|
|
|
|
| Y | 1 | 2 | 3 | 4 |
| fY(y) |
|
|
|
|
| Z | 3 | 4 | 5 | 6 | 7 |
| f(z) |
|
|
|
|
|
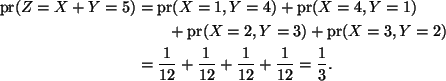
There are six points in the sample space
| number | |
| guess | correct |
| A B C | 3 |
| B C A | 0 |
| C A B | 0 |
| C B A | 1 |
| B A C | 1 |
| A C B | 1 |
| X | 0 | 1 | 2 | 3 |
| f(x) |
|
|
0 |
|
There are
![]() points in the sample space (ways to choose 3 eggs
from 12 eggs).
points in the sample space (ways to choose 3 eggs
from 12 eggs).
Similarly, there are are
![]() to choose k rotten eggs from the
2 rotten eggs in the carton and
to choose k rotten eggs from the
2 rotten eggs in the carton and
![]() to choose k non-rotten
eggs from the 10 non-rotten eggs in the carton. If there are k rotten
eggs drawn, there are 3 - k non-rotten eggs drawn. Thus
to choose k non-rotten
eggs from the 10 non-rotten eggs in the carton. If there are k rotten
eggs drawn, there are 3 - k non-rotten eggs drawn. Thus