University of Minnesota, Twin Cities School of Statistics Stat 3011 Rweb Textbook (Wild and Seber)
For an example we will use the data for Example 12.3.1 in Wild and Seber,
which is in the file
cmputer1.txt.
This file contains three variables. The two of interest in this problem
are no, the number of computer terminals, and pertask,
the time per task (p. 104 and p. 511 in Wild and Seber). The
following R commands
Since the output is rather complicated, we copy it below with the regression coefficients highlighted. The least-squares regression line is
y = 3.04963 + 0.26034 x
Rweb:> summary(out)
Call:
lm(formula = pertask ~ no)
Residuals:
Min 1Q Median 3Q Max
-3.5631 -0.7923 -0.1547 1.3844 2.4403
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.04963 1.26045 2.419 0.0323 *
no 0.26034 0.02705 9.625 5.41e-07 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.672 on 12 degrees of freedom
Multiple R-Squared: 0.8853, Adjusted R-squared: 0.8758
F-statistic: 92.63 on 1 and 12 degrees of freedom, p-value: 5.406e-07
A test of whether a regression coefficient is zero can be read off the regression printout. No additional work required.
We repeat here the same printout as in the preceding section, but here the test statistic and P-value for a test of the hypotheses
Rweb:> summary(out)
Call:
lm(formula = pertask ~ no)
Residuals:
Min 1Q Median 3Q Max
-3.5631 -0.7923 -0.1547 1.3844 2.4403
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.04963 1.26045 2.419 0.0323 *
no 0.26034 0.02705 9.625 5.41e-07 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.672 on 12 degrees of freedom
Multiple R-Squared: 0.8853, Adjusted R-squared: 0.8758
F-statistic: 92.63 on 1 and 12 degrees of freedom, p-value: 5.406e-07
The P-value read off the printout P = 5.41e-07 (meaning 5.4 times 10 to the minus 7) is exceedingly small. So there is a "highly statistically significant" linear relationship between the two variables.
R has no procedure especially for producing confidence intervals for regression coefficients. However, all the information necessary is in the regression printout. Again we repeat the same regression printout, this time with the information necessary for doing a confidence interval for the slope highlighted.
Rweb:> summary(out)
Call:
lm(formula = pertask ~ no)
Residuals:
Min 1Q Median 3Q Max
-3.5631 -0.7923 -0.1547 1.3844 2.4403
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.04963 1.26045 2.419 0.0323 *
no 0.26034 0.02705 9.625 5.41e-07 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.672 on 12 degrees of freedom
Multiple R-Squared: 0.8853, Adjusted R-squared: 0.8758
F-statistic: 92.63 on 1 and 12 degrees of freedom, p-value: 5.406e-07
In the Estimate column is the estimate of the slope.
In the Std. Error column is the standard error of this estimate.
We multiply the standard error by a t critical value derived from
a t distribution with 12 degrees of freedom (n - 2, but we
can also read that directly off the regression printout). Thus
give the margin of error and the interval estimate for the true slope of the population regression line associated with a 95% confidence level.
To get a different confidence level, you would use a different argument
in the qt function.
R also has no procedure especially for performing general hypothesis tests for regression coefficients. The P-value for the test of whether a regression coefficient is zero is given in the regression printout. If we want to test any nonzero hypothesized value for a regression coefficient, we have to do it "by hand" (assisted perhaps by the computer).
Again, all the information necessary is in the regression printout. In fact we use exactly the same information that was highlighted in the preceding printout. We just use it in a different way.
For an example we will use the data for Example 12.4.3 in Wild and Seber,
which is in the file
gauge.txt.
This file contains three variables. The two of interest in this problem
are can and gauge.
The R statements
do the plot shown on p. 530 in Wild and Seber and give the accompanying regression printout, which does not match the regression printout on that page.
The regression printout on p. 530 in Wild and Seber corresponds to the following regression, which deletes case 35 on the grounds that it is an apparent outlier.
Again, we present the R regression output with the relevant numbers highlighted.
Rweb:> summary(out)
Call:
lm(formula = gauge[-35] ~ can[-35])
Residuals:
Min 1Q Median 3Q Max
-0.074413 -0.020389 -0.008787 0.021637 0.132076
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.034438 0.007612 4.524 3.37e-05 ***
can[-35] 0.439803 0.003649 120.519 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.04156 on 54 degrees of freedom
Multiple R-Squared: 0.9963, Adjusted R-squared: 0.9962
F-statistic: 1.452e+04 on 1 and 54 degrees of freedom, p-value: 0
As usual, the test statistic is
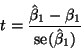
give the test statistic (which agrees with the book) and the one-tailed and two-tailed P-values (which don't exactly). The book is apparently wrong here, but since no details are given of exactly how they got their number (they say "the two-sided P-value is 0.98"), we can't resolve the discrepancy.
Note: This example was not covered in class and won't be on the test or homework. I've just left it on this web page to have it written down somewhere.
For an example we again use the data for Example 12.3.1 in Wild and Seber,
which is in the file
cmputer1.txt.
This file contains three variables. The two of interest in this problem
are no and time.
Now we want to fit a quadratic model and see if it fits better than the linear model. The following R commands
A couple of fine points.
I( ) is used to indicate that no^2
means what it appears to, the square of the variable no.
Otherwise R treats ^ as a magic character meaning something
quite different, as explained on the on-line help for
model
formulas.
no in
curve(predict(out, data.frame(no=x)), add=TRUE)
with the actual name of the predictor variable in the regression actually done.
The regression printout is repeated below with the coefficient of the quadratic term highlighted and also the P-value for testing whether this coefficient is nonzero.
Rweb:> summary(out)
Call:
lm(formula = time ~ no + I(no^2))
Residuals:
Min 1Q Median 3Q Max
-2.3254 -0.6556 -0.0973 1.0512 1.8757
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.215067 1.941166 0.111 0.91378
no 0.036714 0.100780 0.364 0.72254
I(no^2) 0.004526 0.001209 3.745 0.00324 **
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.319 on 11 degrees of freedom
Multiple R-Squared: 0.9715, Adjusted R-squared: 0.9663
F-statistic: 187.7 on 2 and 11 degrees of freedom, p-value: 3.159e-09
The actual value of the coefficient 0.004526 is small, but highly statistically significant (P = 0.003). Hence we conclude that the quadratic model is better and that the linear model is inadequate.
The regression function
![]() is also a parameter of interest. A standard problem asks for
an estimate of this parameter for some particular value of x.
is also a parameter of interest. A standard problem asks for
an estimate of this parameter for some particular value of x.
The predict function in R also does this.
We return to the data used in the
first section of this page
(Example 12.3.1 in Wild and Seber,
data file
cmputer1.txt with variables no and pertask).
The top of p. 533 in Wild and Seber has the estimate of the regression
function for no = 70. The following R statements do this.
As always, the on-line help for the function in question, here predict, gives optional arguments and other information about the function.
In particular, the optional argument level=0.90 changes the
confidence level to 90%.
This section is very similar to the preceding section. The only difference
is the optional argument interval is changed to
interval="prediction".
This gives a prediction interval that has a specified probability
(95% by default) of covering a new data value associated with a specified
predictor value.
The prediction interval at the top of p. 533 in Wild and Seber for
a new pertask value associated with no = 70
is produced by the following R statements.
Yet again we reuse the data used in
first section of this page
(Example 12.3.1 in Wild and Seber,
data file
cmputer1.txt with variables no and pertask).
The R statements
do a QQ plot of the residuals.
For the same data, the R statements
do a plot of the residuals versus the fitted values.
Again, for the same data, the R statements
do a plot of the residuals versus the predictor variable
no.
The plots in this section and the preceding section are essentially the same for simple linear regression. The difference between them only arises in multiple regression (which we haven't done). If there are k predictor variables, then there are k residuals versus predictor plots (one for each of the k predictors, but only one residuals versus fitted values plot. Since the latter shows most of what you want, it is preferred. Certainly, if you are going to make only one plot of this type, it should be a residuals versus fitted values plot.
For an example we will use the data for Example 12.4.1 in Wild and Seber,
which is in the file
rating2.txt.
This file contains two variables: parent and teacher.
For comparison with the correlation analysis, we first do a regression analysis, reproducing the analysis in Example 12.4.1.
Now we return to Section 12.5 in Wild and Seber, where we just want to
examine the correlation of these two variables. The R function
that calculates correlations is cor.
This does produce the correlation 0.2970181 found in Wild and Seber.
If we want to test whether the correlation is zero, we look at the test whether the regression slope is zero. Both are exactly the same test, because the correlation is zero if and only if the regression slope is zero.
Thus the P-value for the test of whether the correlation is zero can be read out of the regression printout of the preceding Rweb submission
Rweb:> summary(out)
Call:
lm(formula = teacher ~ parent)
Residuals:
Min 1Q Median 3Q Max
-27.936 -13.562 -1.398 11.688 49.945
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.3659 11.3561 0.120 0.9047
parent 0.4188 0.1799 2.328 0.0236 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 16.85 on 56 degrees of freedom
Multiple R-Squared: 0.08822, Adjusted R-squared: 0.07194
F-statistic: 5.418 on 1 and 56 degrees of freedom, p-value: 0.02357