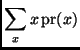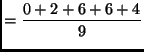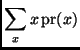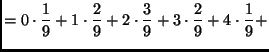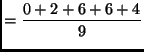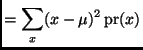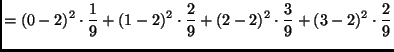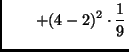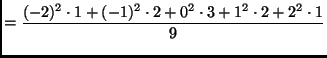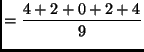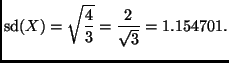Up: Stat 3011
Stat 3011 Midterm 1 (Class Part)
These are described in Section 1.1.2 in Wild and Seber.
- selection bias
- The sample is not representative of the population
because of the method of selection (some form of systematic, non-random
sampling).
- nonresponse bias
- The nonresponders (individuals who do not return
questionaires, who are not in when the interviewer calls, or who do not
answer some questions) are different from responders.
- self-selection
- (a special case of selection bias) individuals
surveyed themselves choose to be in the sample (instant TV polls, internet
polls, hotel and restaurant customer satisfacation forms).
- question effects
- Wording of questions strongly influences answers.
- survey-format effects
- Order of questions, length of survey, and
general instructions applying to all questions can influence answers.
- interviewer effects
- Interviewer tone of voice or facial expression can
influence answers.
- social desirability bias
- Some respondents are reluctant to give
answers or admit to behavior that is generally considered socially
undesirable.
The mean is
The standard deviation is
where 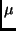 is the mean calculated in part (a), and
is the mean calculated in part (a), and
Thus
You can't use the addition rule here because the events are not mutually
exclusive (independent events aren't mutually exclusive). Thus some
combination of the multiplication rule and complement rule must do the job.
The multiplication rule doesn't directly calculate events of the form
``at least one'' so we must use the complement rule first. The
complementary event of ``at least one'' is ``none,'' that is, the gambler
loses all 10. And that is the kind of event that the multiplication rule
handles
because all the bets have the same probability of a win or a loss.
By another application of the complement rule
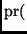
loses any one
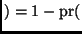
wins any one
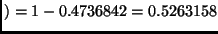
Hence
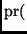
loses any one
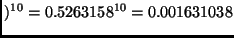
and
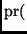
wins at least one
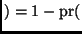
loses all 10
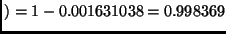
Note: same as part (c) because
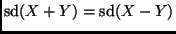 .
.



Up: Stat 3011
Charles Geyer
2001-10-22