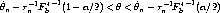Handout
for
Stat
5601
Subsampling Bootstrap Confidence Intervals
The fundamental idea of the subsampling bootstrap is that
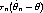 | (1) |
converges in distribution to some distribution (any distribution!). Trivially,
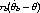 | (2) |
converges to the same distribution, since whether we index by n or b is merely a
matter of notation. Usually, we write (2) as
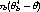 | (3) |
to distinguish the estimator 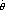 n for the full data and the estimator
n for the full data and the estimator  b* for a
subsample.
The basic assumptions of the subsampling bootstrap are
b* for a
subsample.
The basic assumptions of the subsampling bootstrap are
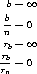 | (4) |
where n is the sample size and b the subsample size.
Under these assumptions
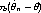 | (5) |
converges in probability to zero, just because we would need to multiply by  n rather
than
n rather
than  b to get a nonzero limit and
b to get a nonzero limit and  b/
b/ n goes to zero (those who had the theory class
may recognize that this was a homework problem).
Subtracting (5) from (3) gives
n goes to zero (those who had the theory class
may recognize that this was a homework problem).
Subtracting (5) from (3) gives
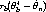 | (6) |
which has the same limit as (3) or (1) (those who had the theory course may
recognize that this is because of Slutsky’s theorem).
To summarize where we have gotten to, the subsampling bootstrap is based on
the assumptions (4) and that (1) converges in distribution to something. In which
case, it follows from asymptotic theory that (6) converges to the same limiting
distribution as does (1).
It does not matter what the limiting distribution is because we will approximate
it using the subsampling bootstrap. Suppose the limiting distribution has distribution
function F. We don’t know the functional form of F but we can approximate it
by the empirical distribution function Fb* of the bootstrap (sub)samples
(6).
We know that for large n
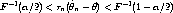 | (7) |
occurs with probability approximately 1 -  . That’s what convergence in distribution
of (1) to the distribution with distribution function F means. F-1(
. That’s what convergence in distribution
of (1) to the distribution with distribution function F means. F-1( /2) is the
/2) is the  /2
quantile of this distribution and F-1(1 -
/2
quantile of this distribution and F-1(1 -  /2) is the 1 -
/2) is the 1 -  /2 quantile. Thus if Y is a
random variable having this distribution and the distribution is continuous, the
probability that
/2 quantile. Thus if Y is a
random variable having this distribution and the distribution is continuous, the
probability that
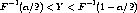 | (8) |
is 1 -  . Since we are assuming Y and
. Since we are assuming Y and  n(
n(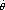 n -
n -  ) have approximately the
same distribution for large n, (7) has approximately the same probability as
(8).
Of course, we don’t know F, but Fb* converges to F, so for large b and n, we
have
) have approximately the
same distribution for large n, (7) has approximately the same probability as
(8).
Of course, we don’t know F, but Fb* converges to F, so for large b and n, we
have
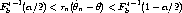 | (9) |
with probability 1 -  . Rearranging (9) to put
. Rearranging (9) to put  in the middle by itself gives
in the middle by itself gives
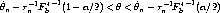 | (10) |
which is the way subsampling bootstrap confidence intervals are done.
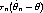
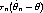
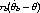
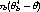
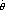 n for the full data and the estimator
n for the full data and the estimator  b* for a
subsample.
The basic assumptions of the subsampling bootstrap are
b* for a
subsample.
The basic assumptions of the subsampling bootstrap are 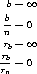
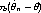
 n rather
than
n rather
than  b to get a nonzero limit and
b to get a nonzero limit and  b/
b/ n goes to zero (those who had the theory class
may recognize that this was a homework problem).
Subtracting (5) from (3) gives
n goes to zero (those who had the theory class
may recognize that this was a homework problem).
Subtracting (5) from (3) gives 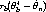
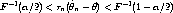
 . That’s what convergence in distribution
of (1) to the distribution with distribution function F means. F-1(
. That’s what convergence in distribution
of (1) to the distribution with distribution function F means. F-1( /2) is the
/2) is the  /2
quantile of this distribution and F-1(1 -
/2
quantile of this distribution and F-1(1 -  /2) is the 1 -
/2) is the 1 -  /2 quantile. Thus if Y is a
random variable having this distribution and the distribution is continuous, the
probability that
/2 quantile. Thus if Y is a
random variable having this distribution and the distribution is continuous, the
probability that 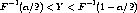
 . Since we are assuming Y and
. Since we are assuming Y and  n(
n(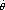 n -
n -  ) have approximately the
same distribution for large n, (7) has approximately the same probability as
(8).
Of course, we don’t know F, but Fb* converges to F, so for large b and n, we
have
) have approximately the
same distribution for large n, (7) has approximately the same probability as
(8).
Of course, we don’t know F, but Fb* converges to F, so for large b and n, we
have 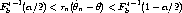
 . Rearranging (9) to put
. Rearranging (9) to put  in the middle by itself gives
in the middle by itself gives