Stat 3011 Midterm 2 (Class Part)

Problem 1

A confidence interval is an estimate of a parameter (some population characteristic). It may or may not contain the parameter. The probability that a 95% confidence interval covers the parameter is (or at least should be) 95%. we know is that, in general, 95% of such intervals are right (contain the true parameter value and 5% are wrong (do not contain the true parameter value). But we do not know and can never know whether this particular interval (0.41, 0.55) is among the lucky 95% or the unlucky 5%.

Problem 2

(a)

The confidence interval is

$$\bar{x} \pm (\text{critical value}) \frac{s}{\sqrt{n}}$$

In this problem

$$\begin{split} \bar{x} & = 11.7 \\ s & = 2.3 \\ n & = 40 \end{split}$$

The only issue is what to use for the critical value. Since n is fairly large 2 will do (as we used in Chapter 7) or 1.96 or 2.023 (from the table of t critical values, Appendix 6 in Wild and Seber, for n - 1 = 39 degrees of freedom). The three choices give confidence intervals

$$\begin{split} 11.7 & \pm 0.7127774 \\ 11.7 & \pm 0.7273239 \\ 11.7 & \pm 0.7356881 \end{split}$$

The standard errors should be rounded to two significant figures (Section 7.4.3 in Wild and Seber) giving 0.71 or 0.73 or 0.74 for the plus or minus.

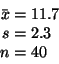
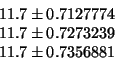
The rules for rounding intervals in the same section, say the last digit of the interval should be about one more digit than the width of the interval, so first decimal place, thus all three critical values give the same rounded interval (11.0, 12.4).

(b)

You need to assume that n = 40 is large enough so that the sampling distribution of $X{\mkern -13.5 mu}\overline{\phantom{\text{X}}}$ is approximately normal, which it will be unless the population distribution is very skewed.

(c)

The z critical value for 90% would be 1.645. The t critical value would be 1.685 ( n - 1 = 39 degrees of freedom). It doesn't make much difference which you use. Everything else is the same.

(d)

For a sample size this small you must use a t critical value, which is 2.262 (n - 1 = 9 degrees of freedom). And $\sqrt{n}$ is $\sqrt{10}$ rather than $\sqrt{40}$. Everything else is the same.

(e)

For the interval to be exact, you need to assume the population distribution is exactly normal. For it to be approximately correct, you need to assume the population distribution is close to normal. The sample size isn't large enough for the central limit theorem to make the sampling distribution of $X{\mkern -13.5 mu}\overline{\phantom{\text{X}}}$ approximately normal despite a non-normal population distribution.

Problem 3

The confidence interval is

$$\hat{p}_1 - \hat{p}_2 \pm (\text{critical value}) \mathop{\rm se}\nolimits(\hat{p}_1 - \hat{p}_2)$$

which is

$$\hat{p}_1 - \hat{p}_2 \pm (\text{critical value}) \sqrt{\fra... ...1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2 (1 - \hat{p}_2)}{n_2}}$$

Since n₁ and n₂ are large a z critical value is appropriate (a t critical value is never appropriate for proportions) either 1.96 or 2 will do. The two choices give confidence intervals

$$\begin{split} 0.076 & \pm 0.06788734 \\ 0.076 & \pm 0.0692728 \end{split}$$

The standard errors should be rounded to two significant figures (Section 7.4.3 in Wild and Seber) giving 0.068 or 0.069 for the plus or minus.

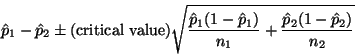
The rules for rounding intervals in the same section, say the last digit of the interval should be about one more digit than the width of the interval, so third decimal place, the rounded intervals are

(0.008, 0.144)
(0.007, 0.145)

Problem 4

The formula for the required sample size is given the box on p. 353 in Wild and Seber

$$n \approx \left(\frac{z \sigma^*}{m}\right)^2$$

where z is the critical value (1.96 or 2 for 95%), $\sigma^*$ is a guesstimate of the standard deviation (use the 0.065 given in the problem statement), and m is the desired margin of error (0.01), so

$$n \approx \left(\frac{1.96 \times 0.065}{0.01}\right)^2 = 162.3$$

(That's a lot. The chemist will probably settle for a larger margin of error or a lower confidence level.)