


Up: Stat 5102
Stat 5102 Second Midterm ExamApril 13, 2001
Name Student ID
The exam is open book, including handouts. It is closed notes.
You may use one
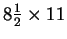 sheet of paper with formulas, etc.
You may use a calculator.
sheet of paper with formulas, etc.
You may use a calculator.
Put all of your work on this test form (use the back if necessary).
Show your work or give an explanation of your answer. No credit
for numbers with no indication of where they came from.
The points for the questions total to 100.
There are ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) pages
and 5 problems.
pages
and 5 problems.
- [20 pts.] Suppose
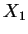 ,
, 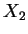 ,
,  are i. i. d.
Beta
are i. i. d.
Beta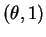 ,
that is the densities are
and suppose the prior distribution for
,
that is the densities are
and suppose the prior distribution for 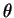 is
Exp
is
Exp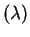 ,
where
,
where 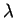 is a hyperparameter (a known constant).
is a hyperparameter (a known constant).
- Find the posterior distribution of
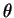 .
.
- Find the posterior mode of
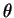 (note: mode, not mean or median).
(note: mode, not mean or median).
- [20 pts.] Suppose data
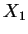 ,
,  ,
, 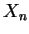 are assumed to be i. i. d. with
Normal
are assumed to be i. i. d. with
Normal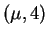 , where
, where 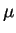 is an unknown parameter.
Suppose we want to do a Bayesian analysis with prior distribution
for
is an unknown parameter.
Suppose we want to do a Bayesian analysis with prior distribution
for 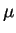 having prior distribution
Normal
having prior distribution
Normal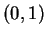 .
.
-
Find the posterior distribution for
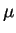 , giving it either as a
normalized probability density function or as a named distribution
with specified values of the hyperparameters.
, giving it either as a
normalized probability density function or as a named distribution
with specified values of the hyperparameters.
-
Find the 95% highest posterior density (HPD) region for
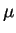 .
.
- [20 pts.]
Let
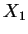 ,
, 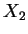 ,
, 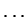 ,
, 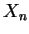 be i. i. d. discrete random variables
having a distribution in the parametric family with probability functions
where
be i. i. d. discrete random variables
having a distribution in the parametric family with probability functions
where
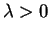 is the parameter.
is the parameter.
- Find the MLE of
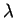 . You do not have to prove that your solution
is the global maximizer of the likelihood. It is enough to find it.
. You do not have to prove that your solution
is the global maximizer of the likelihood. It is enough to find it.
- Find the expected Fisher information for
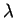 .
.
- Give an asymptotic 95% confidence interval for
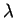 .
.
- [20 pts.]
Suppose
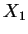 ,
, 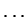 ,
, 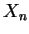 are i. i. d.
Normal
are i. i. d.
Normal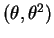 ,
where
,
where 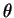 is an unknown parameter, that is,
is an unknown parameter, that is, 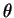 is
both the mean and standard deviation of each
is
both the mean and standard deviation of each 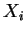 .
.
- Calculate the observed Fisher information
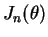 .
.
- Calculate the expected Fisher information
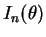 .
.
- [20 pts.] Suppose in a trial of a new cancer drug there were 500 subjects randomly
assigned, 250 to the ``treatment group'' which received the new drug and
250 to the ``control group'' which received the standard therapy.
The results of the trial were that 95 subjects in the treatment group
died (38%) and 116 subjects in the control group died (46.4%).
If 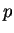 is the true population probability of death under treatment with
the new drug and
is the true population probability of death under treatment with
the new drug and 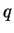 is the true population probability of death under
the standard therapy, conduct a test of the the hypotheses
is the true population probability of death under
the standard therapy, conduct a test of the the hypotheses
giving the 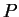 -value for the test.
-value for the test.



Up: Stat 5102
Charles Geyer
2001-04-19
![]() sheet of paper with formulas, etc.
You may use a calculator.
sheet of paper with formulas, etc.
You may use a calculator.
![]() pages
and 5 problems.
pages
and 5 problems.
![]() is the true population probability of death under treatment with
the new drug and
is the true population probability of death under treatment with
the new drug and ![]() is the true population probability of death under
the standard therapy, conduct a test of the the hypotheses
is the true population probability of death under
the standard therapy, conduct a test of the the hypotheses