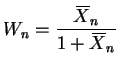Up: Stat 5102
Stat 5102 First Midterm ExamMarch 2, 2001
Name Student ID
The exam is open book, including handouts. It is closed notes.
You may use one
 sheet of paper with formulas, etc.
You may use a calculator.
sheet of paper with formulas, etc.
You may use a calculator.
Put all of your work on this test form (use the back if necessary).
Show your work or give an explanation of your answer. No credit
for numbers with no indication of where they came from.
The points for the questions total to 100.
There are ![[*]](/usr/lib/latex2html/icons.gif/cross_ref_motif.gif) pages
and 5 problems.
pages
and 5 problems.
- [20 pts.]
Suppose
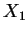 ,
, 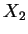 ,
, 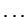 are i. i. d.
are i. i. d.
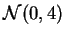 and
and
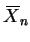 and
and 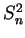 are the sample mean and variance for a sample
of size
are the sample mean and variance for a sample
of size 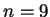 (with
(with 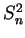 defined as in equation (7.17) in the
notes with
defined as in equation (7.17) in the
notes with 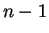 in the denominator).
in the denominator).
Find
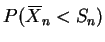 exactly (not approximately).
exactly (not approximately).
- [20 pts.]
Suppose
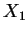 ,
, 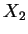 ,
,  are i. i. d. from
the distribution with density
where
are i. i. d. from
the distribution with density
where 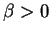 is an unknown parameter.
is an unknown parameter.
Find a method of moments estimator for 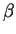 .
.
- [20 pts.]
Suppose
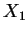 ,
, 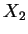 ,
, 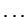 are i. i. d.
are i. i. d.
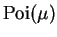 .
Because
.
Because
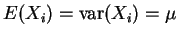 , both the sample mean
, both the sample mean
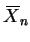 and sample variance
and sample variance 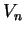 are consistent estimators of
are consistent estimators of 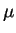 .
.
The fourth central moment of the
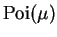 distribution is
distribution is
- Find the asymptotic distribution of
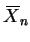 .
(Express all parameters in terms of
.
(Express all parameters in terms of 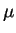 .)
.)
- Find the asymptotic distribution of
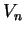 .
(Express all parameters in terms of
.
(Express all parameters in terms of 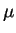 .)
.)
- Find the asymptotic relative efficiency of
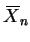 with respect to
with respect to
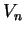 considered as estimators of
considered as estimators of 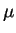 .
.
- State which is the better estimator.
- [20 pts.]
Suppose
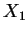 ,
, 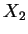 ,
, 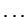 are i. i. d.
are i. i. d.
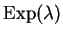 random variables,
where
random variables,
where
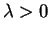 is an unknown parameter.
As usual, let
is an unknown parameter.
As usual, let
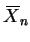 denote the sample mean. What is
the asymptotic distribution of
denote the sample mean. What is
the asymptotic distribution of
- [20 pts.]
Suppose
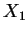 ,
, 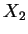 ,
,  are i. i. d.
are i. i. d.
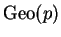 random variables,
where
random variables,
where 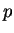 is an unknown parameter such that
is an unknown parameter such that 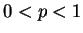 (and by
(and by
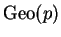 we mean the distribution described by Section B.1.8 of the Appendix on Brand
Name Distributions in the notes).
As usual, let
we mean the distribution described by Section B.1.8 of the Appendix on Brand
Name Distributions in the notes).
As usual, let
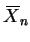 denote the sample mean.
Find an asymptotic 95% confidence interval for
denote the sample mean.
Find an asymptotic 95% confidence interval for 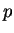 corresponding
to data
corresponding
to data 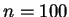 and
and
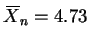 .
.



Up: Stat 5102
Charles Geyer
2001-03-05
![]() sheet of paper with formulas, etc.
You may use a calculator.
sheet of paper with formulas, etc.
You may use a calculator.
![]() pages
and 5 problems.
pages
and 5 problems.
![]() exactly (not approximately).
exactly (not approximately).
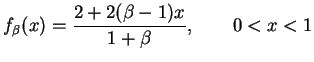
![]() .
.
![]() distribution is
distribution is