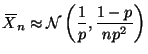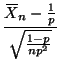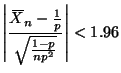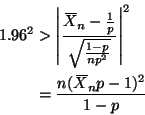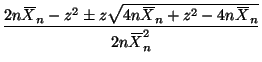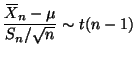
Stat 5102 (Geyer) Midterm 1
The basic fact this problem uses is
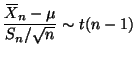
To use (1), we must put the event of interest
![]() in a form related to the left hand side of (1). Clearly, this
is equivalent to
in a form related to the left hand side of (1). Clearly, this
is equivalent to
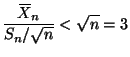
From Table IIIa in Lindgren
![]() ,
so
,
so
![]() .
.
To use the method of moments, we first need to find some moments. Since this is not a ``brand name'' distribution, we must integrate to find the moments. The obvious moment to try first is the first moment (the mean)
![\begin{displaymath}
\begin{split}
\mu
& =
\int_0^1 x f_\beta(x) \, d x
\\
...
...ht]_0^1
\\
& =
\frac{1 + 2 \beta}{3 + 3 \beta}
\end{split}\end{displaymath}](img14.gif)
Either way, we get a method of moments estimator by plugging in
![]() for
for ![]()
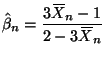
The asymptotic distribution of
![]() is, as usual, by the CLT,
is, as usual, by the CLT,
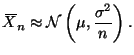
The asymptotic distribution of ![]() is, by
Corollary 7.17 in the notes,
is, by
Corollary 7.17 in the notes,
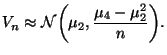
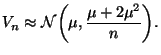
The ARE is the ratio of the asymptotic variances, either ![]() or the the reciprocal
or the the reciprocal
![]() , depending on which way you write it.
, depending on which way you write it.
The better estimator is the one with the smaller asymptotic variance,
in this case
![]() .
.
This is a problem for the delta method. We know from the properties of the exponential distribution
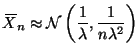
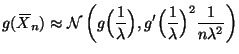
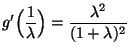
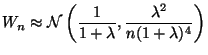
There are several different ways to proceed here.
The mean is
![]() . Thus we could just get a confidence interval
for
. Thus we could just get a confidence interval
for ![]() and take reciprocals of the endpoints to get a confidence interval
for
and take reciprocals of the endpoints to get a confidence interval
for ![]() .
.
A confidence interval for ![]() can be found using Theorem 9.8 in the notes.
From Section B.1.8 of the notes
can be found using Theorem 9.8 in the notes.
From Section B.1.8 of the notes
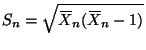
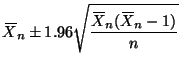
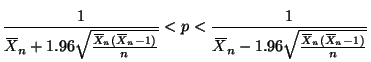
The obvious point estimator for ![]() is
is
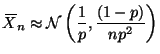
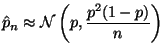
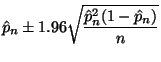
The really hard way to do this problem is to start with