The exam is open book, including handouts. It is closed notes. You may use a calculator.
Put all of your work on this test form (use the back if necessary). Show your work or give an explanation of your answer. No credit for numbers with no indication of where they came from.
The points for the questions total to 100.
There are ![]() pages
and 5 problems.
pages
and 5 problems.
[20 pts.]
Suppose X1, X2, ![]() ,
Xn are i. i. d. discrete random variables
with density
,
Xn are i. i. d. discrete random variables
with density
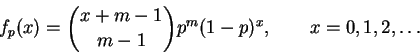
[20 pts.]
Suppose X1, X2, ![]() Xn are i. i. d. from the distribution with
density
Xn are i. i. d. from the distribution with
density
[20 pts.]
Suppose X1, X2, ![]() are i. i. d. from a statistical model
having a single parameter
are i. i. d. from a statistical model
having a single parameter
![]() .
I do not tell you anything about the model other than that the MLE
.
I do not tell you anything about the model other than that the MLE
![]() exists and satisfies the conditions for the usual
asymptotics to hold and that the Fisher information is
exists and satisfies the conditions for the usual
asymptotics to hold and that the Fisher information is
[20 pts.]
Suppose X1, X2, ![]() are i. i. d.
are i. i. d.
![]() distribution, where
distribution, where ![]() and
and ![]() are unknown parameters,
and suppose S2n is the usual sample variance
are unknown parameters,
and suppose S2n is the usual sample variance
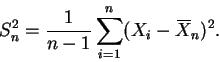
[20 pts.]
Suppose X1, X2, ![]() are i. i. d.
are i. i. d.
![]() random
variables and, as usual,
random
variables and, as usual,
![]() denotes the sample mean.
Perform an asymptotic (large sample) test of the hypotheses
denotes the sample mean.
Perform an asymptotic (large sample) test of the hypotheses
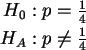
corresponding to sample size n = 100 and sample mean
![]() .
Give the P-value for the test and also say whether H0 is accepted
or rejected at the .05 level of significance.
.
Give the P-value for the test and also say whether H0 is accepted
or rejected at the .05 level of significance.