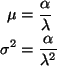
so
and the CLT says
Stat 5102 (Geyer) Final Exam
First define
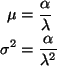
so
![]()
and the CLT says
Now we apply the delta method to the transformation
Let's look at the simplest moment first
An asymptotic test can be based on the asymptotically pivotal quantity
Since P < 0.05, reject H0.
First we have to find the posterior. The relevant formulas are given
in Example 5.2.4 in the notes, equations (5.17a) and (5.17b).
The precision of the data distribution is
1 / 25 = 0.04 and the
prior precision is
1 / 10 = 0.10. Hence from (5.17a) the posterior
precision is
The HPD region is
The model called ``Model 1'' in the ANOVA table has regression
function
The table gives a P-value P = 0.004277 for the test of model comparison. Since the P-value is very small, this is strong evidence against the small model. Thus we conclude that the piecewise linear model fits and the simple linear model (``Model 1'') doesn't.
This problem was a learning experience for the teacher. We needed some homework problems like this. It was harder than I thought it would be. Most people had no clear idea of how to show the models were nested. Only two people got full credit.
In order two show the models are nested, you need to show one of two things.
These two conditions come to much the same thing (as we shall see below).
We can write the regression functions for the little model
A little thought suggests
![]() ,
which collapses the
two cases in (1) to one
,
which collapses the
two cases in (1) to one
The design matrices for the two models are
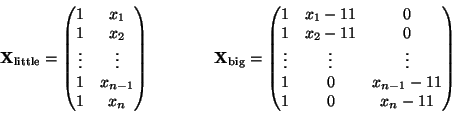
The density of the data is
The likelihood for a sample of size n is
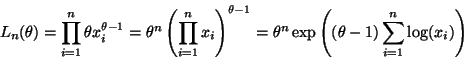
Sanity Check: Does this make sense? Are both parameters of
the posterior positive? Clearly
![]() is positive, because
we need
is positive, because
we need
![]() for the prior to make sense. How
about
for the prior to make sense. How
about
![]() ? At first sight this doesn't look positive.
We need
? At first sight this doesn't look positive.
We need
![]() for the prior to make sense, but how do we know that
the other bit doesn't make it negative? Have to think a bit.
0 < xi < 1,
so
for the prior to make sense, but how do we know that
the other bit doesn't make it negative? Have to think a bit.
0 < xi < 1,
so
![]() (logs of numbers less than one are negative), so
(logs of numbers less than one are negative), so
![]() is actually positive despite its appearance, and
everything is o. k.
is actually positive despite its appearance, and
everything is o. k.
The regression coefficient in question is -0.011464 and R gives its standard error as 0.007784 and the degrees of freedom for error as 17. We only need to look up the t critical value from Table IIIb in Lindgren, which for 90% confidence is 1.74 (note not in the column headed 90, but in the next one over that has 1.645 as the appropriate z critical value at the bottom).
Thus the interval is
The sample median
![]() is asymptotically normal center
m the population median and variance
1 / 4 n f(m)2 (Corollary 2.28
in the notes). Here the population median is zero by symmetry and
is asymptotically normal center
m the population median and variance
1 / 4 n f(m)2 (Corollary 2.28
in the notes). Here the population median is zero by symmetry and
![]() .
Hence
.
Hence