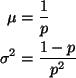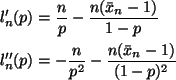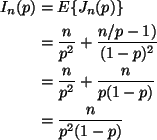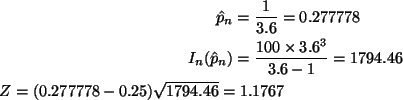Up: Stat 5102
Stat 5102 (Geyer) Midterm 2
The likelihood is
and the log likelihood is
The derivatives are
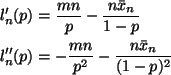
Since the second derivative is negative for all p, the log likelihood
is a strictly concave and there is at most one local maximum, which is the
MLE and the point where the first derivative is zero, if such a
point exists. Setting the first derivative to zero and solving for pgives
The observed Fisher information is just
- ln''(p)
This is much simpler than calculating expectations or variances.
The asymptotic confidence interval using observed Fisher information is
If you want to simplify that
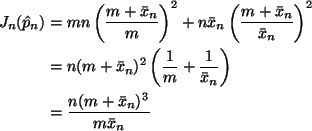
However, that is not necessary for full credit.
Calculating expected Fisher information in part (b) is not advisable
unless you recognize that the distribution of the Xi is related
to a negative binomial distribution. In fact
So we can look up (equation (7) on p. 156 in Lindgren)
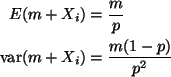
which can be used to calculate expected Fisher information by either
method (variance of the first derivative of log likelihood or minus the
expectation of the second derivative).
We'll just do the second here
So
When we evaluate at the MLE, we actually get the same thing as
with observed Fisher information, that is,
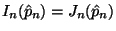 .
.
The likelihood is
where to simplify notation we have defined the statistic
The prior is
so likelihood times prior is
which (considered as a function of 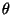 )
is an unnormalized
)
is an unnormalized
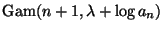 density. Thus that's the posterior.
density. Thus that's the posterior.
The mean of a gamma is the shape parameter divided by the scale parameter
This is a job for Corollary 4.10 in the notes.
The inverse transformation is
which has derivative
Thus the Fisher information for 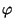 is
is
or if you prefer
where, of course
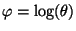 is the true parameter value.
is the true parameter value.
Part (b) could also be done using the delta method,
but that wouldn't reuse part (a).
An exact test is based on the pivotal quantity
To make a test statistic, we plug in the parameter value hypothesized
under the null hypothesis
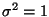 giving a test statistic
T = 9 * 2.3 / 1 = 20.7.
giving a test statistic
T = 9 * 2.3 / 1 = 20.7.
The P-value is
P(Y > 20.7) where
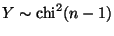 .
From Table Va in Lindgren, this is between 0.014 and 0.015,
say P = 0.015. (R says P = 0.014.) Since P < 0.05 the null
hypothesis is rejected at the 0.05 level of significance.
.
From Table Va in Lindgren, this is between 0.014 and 0.015,
say P = 0.015. (R says P = 0.014.) Since P < 0.05 the null
hypothesis is rejected at the 0.05 level of significance.
The easiest asymptotic test is based on the asymptotically pivotal quantity
which is approximately standard normal for large n. To do the test in
this particular problem we need to plug in the mean and standard deviation
of the geometric distribution (from pp. 154-155 in Lindgren)
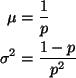
So under H0
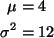
giving a value of
The one-tailed P-value is
P(Z < -1.1547) where Z is standard normal.
From Table I in Lindgren, this is between 0.1251 and 0.1230, say P = 0.124.
Of course, here we are doing a two-tailed test, for which the P-value
is twice this P = 0.248. Since P > .05 we accept H0 at the 0.05
level of significance.
This was not intended as a likelihood inference problem, but you can make it
one. The likelihood is
and the log likelihood is
with derivatives
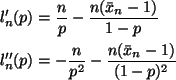
Since the second derivative is negative for all p, the log likelihood
is a strictly concave and there is at most one local maximum, which is the
MLE and the point where the first derivative is zero, if such a
point exists. Setting the first derivative to zero and solving for pgives
The observed Fisher information is
Since
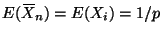 ,
the expected Fisher information is
,
the expected Fisher information is
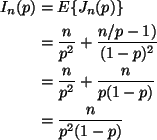
Although these look a bit different, they are the same when evaluated
at the MLE
The asymptotically pivotal quantity we use to make a test is
which is approximately standard normal for large n. Here is
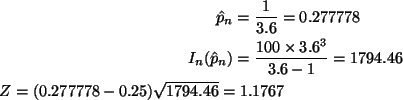
Almost the same Z as in the simpler method (the two procedures
are asymptotically equivalent). The two-tailed P-value is
P = 0.2394 and again H0 is accepted at the 0.05 level of significance.



Up: Stat 5102
Charles Geyer
2000-04-17
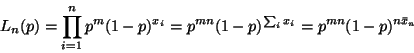
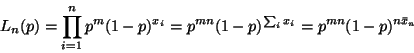
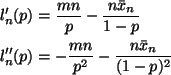
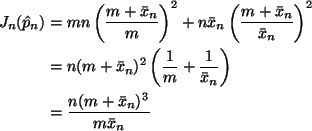
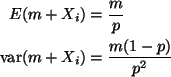
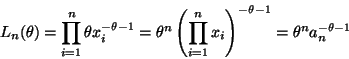
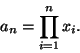
![]() .
From Table Va in Lindgren, this is between 0.014 and 0.015,
say P = 0.015. (R says P = 0.014.) Since P < 0.05 the null
hypothesis is rejected at the 0.05 level of significance.
.
From Table Va in Lindgren, this is between 0.014 and 0.015,
say P = 0.015. (R says P = 0.014.) Since P < 0.05 the null
hypothesis is rejected at the 0.05 level of significance.