Stat 5102 (Geyer) Midterm 1
The basic fact this problem uses is
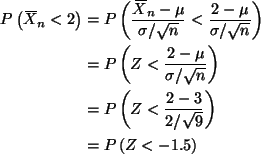
To use the method of moments, we first need to find some moments.
Since this is not a ``brand name'' distribution,
we must integrate to find the moments.
The obvious moment to try first is the first moment (the mean)
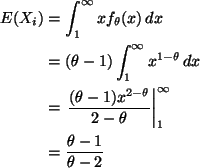
Solving for ![]() as a function of
as a function of ![]() ,
we get
,
we get
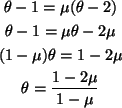
or perhaps it would be nicer to write
A lot of students had trouble doing the moment integral. Either they
didn't have the pattern clear in their minds
This is a symmetric distribution (draw a picture of the density)
with center of symmetry
![]() .
Hence
.
Hence ![]() is both the mean and the median of the population distribution,
and both
is both the mean and the median of the population distribution,
and both
![]() and
and
![]() are consistent and asymptotically
normal estimators of
are consistent and asymptotically
normal estimators of ![]() .
So this question makes sense.
.
So this question makes sense.
The asymptotic distribution of
![]() is, as usual, by the CLT,
is, as usual, by the CLT,
The asymptotic distribution of
![]() is, as usual, by
Corollary 2.28 in the notes,
is, as usual, by
Corollary 2.28 in the notes,
By the comments preceeding part (a),
![]() ,
and
by the formula for the density given in the problem statement
,
and
by the formula for the density given in the problem statement
![]() .
Hence
.
Hence
The ARE is the ratio of the asymptotic variances, either
The better estimator is the one with the smaller asymptotic variance,
in this case
![]() .
.
Several people got an n in their expression for ARE. This can never
happen. ARE is defined as the ratio of asymptotic variances, which do
not contain n. If you messed this up, you either forgot an n somewhere
or got confused between the two forms of asymptotic expressions. In the
mathematically precise forms
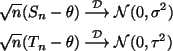
(this is copied from p. 86 in the notes), the ARE of Sn to Tn is
![]() .
Note that neither contains an n. No limit
of any sort contains an n. In the sloppy forms
.
Note that neither contains an n. No limit
of any sort contains an n. In the sloppy forms
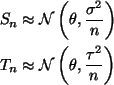
Both variances are proportional to 1 / n and the ratio is
![]() as before, the n's cancel.
as before, the n's cancel.
Even in the tricky case where one of the estimators does not obey the
square root law, e. g., mean versus median for Cauchy or mean versus
X(n) for
![]() ,
the ARE still does not
contain an n, it would be zero or infinity. An ARE with an n in it
is always wrong.
,
the ARE still does not
contain an n, it would be zero or infinity. An ARE with an n in it
is always wrong.
This is a job for Theorem 3.12 in the notes.
The problem doesn't specify an equal-tailed interval (
![]() in the theorem), but that's the most common, so that's what this solution
will do. Note that as the comment immediately following the theorem says
n Vn = (n - 1) S2n so we use the theorem with that plugged in.
in the theorem), but that's the most common, so that's what this solution
will do. Note that as the comment immediately following the theorem says
n Vn = (n - 1) S2n so we use the theorem with that plugged in.
Our confidence interval for ![]() is
is
This is a problem for the delta method. We know from the properties
of the exponential distribution
Many students got the calculus wrong. They didn't even give themselves a chance to do it right. You can't differentiate a function when you aren't clear what the function is. You must have (1) written down in order to have a chance of producing (2).
Of course the letter x in (1) is a dummy variable. It is perfectly
o. k. to write
g(u) = e- t / u or
![]() or
the same thing with any other letter substituted for x on both sides
of (1). What you can't do is try to differentiate something like
or
the same thing with any other letter substituted for x on both sides
of (1). What you can't do is try to differentiate something like
In order to differentiate a function, you have to know what it is. Write down a correct definition.
Many students got the asymptotic variance wrong for another reason.
The got confused between the ``precise'' and ``sloppy'' asymptotic expressions.
The univariate delta method says, if